基础

正向传播

两层神经网络

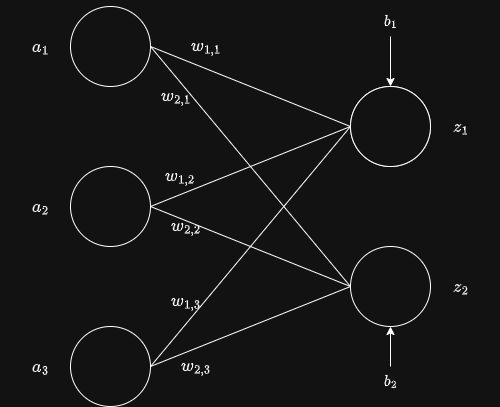
向量形式与分量形式

$$\begin{gathered} z=g(w\ast a+b) \\ {z}_1=g(a_1\ast w_{1,1}+a_2\ast w_{1,2}+a_3\ast w_{1,3}+b_1) \\ {z}_2=g(a_1\ast w_{2,1}+a_2\ast w_{2,2}+a_3\ast w_{2,3}+b_2) \end{gathered}$$

其中$w_{1,2}$代表后一层第1个神经元与前一层第2个神经元连接的权重。

输入向量为

$$a=[a_1,a_2,a_3]$$

权重矩阵为

$$w=\left[\begin{array}{ccc}{W}_{1,1}& W_{1,2}& W_{1,3}\\ W_{2,1}& W_{2,2}& W_{2,3}\end{array}\right]$$

多层神经网络

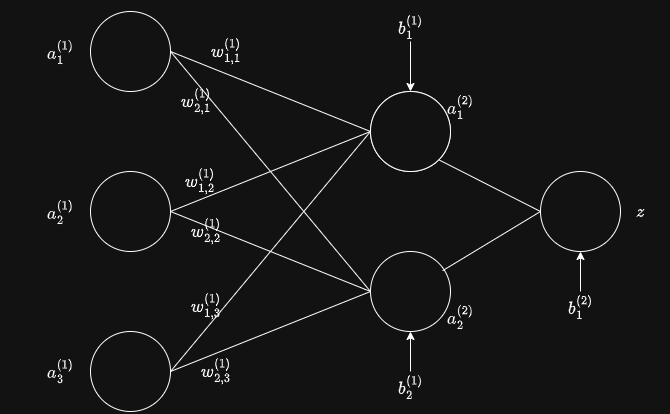
多层神经网络还需要上标来区分层

激活

如果神经网络中都是线性运算，则堆叠层数无用，均可化简为线性方程组。而激活就是将线性加权结果进行一个非线性变换

常见激活函数：sigmoid、tanh、relu、leaky relu、softmax等

训练

已知输入的a和输出的z，通过反向传播求解权重w和偏置b，最终实现输入a得到输出接近真实值的z。

损失

损失loss = 预测值与真实值的差异（数值差异、概率差异、分布差异）= L(w,b)

如此，将问题转换为一个优化问题，即w，b取何值时L(w, b)最小。

Pytorch创建tensor

官方教程

cuda、cudnn、pytorch安装过程省略，假设已经安装好

import torch
print(torch.__version__)
print(torch.cuda.is_available())

x = torch.empty(5, 3, dtype=torch.float64)

# 让x的每个元素都为1
x = x.new_ones(5, 3, dtype=torch.float64)

y = torch.tensor([1, 2, 3])

# 生成一个形状为y的tensor，每个元素都随机
y = torch.randn_like(y, dtype=torch.float)

print(x)
print(y)
print(x.size())
print(x + y)
print(torch.add(x, y))

result = torch.empty(5, 3)
torch.add(x, y, out=result) # out参数
print(result)


y.add_(x[0, :]) # 形状相同才能add
print(y)

# 改变tensor形状
y = x.view(15)
z = x.view(-1, 5) # -1表示该维度的长度自动计算
print(x.size(), y.size(), z.size())

Pytorch 自动微分实现

想了解原理，请参考自动微分原理，以下为实操教程

backward

在Pytorch中，可以使用如下函数进行求导

torch.autograd.backward(self, gradient=None, retain_graph=None, create_graph=False, inputs=None)
# gradient: 如果张量是非标量（即其数据有多个元素）且需要梯度，则backward函数还需要指定“梯度”。它应该是类型和位置都匹配的张量。
# retain_graph: 如果设置为False，用于计算梯度的图形将被释放。通常在调用backward后，会自动把计算图销毁，如果要想对某个变量重复调用backward，需要将该参数设置为True。
# create_graph: 当设置为True的时候可以用来计算更高阶的梯度。
# inputs ：需要计算梯度的张量。如果没有提供，则梯度被累积到所有叶子张量上。
# 需要注意的是，这个函数只是提供求导功能，并不返回值，返回的总是None。

如果Tensor类表示的是一个标量，则不需要为backward()指定任何参数，具体操作如下

a = torch.tensor(1.0, requires_grad=True)
b = torch.tensor(2.0, requires_grad=True)
z = x**3+b
z.backward()
print(z, a.grad, b.grad)

# 如果使用inputs参数，比如：
torch.autograd.backward([z], inputs=[a])
# 则只会在 a 上累积，b上不会计算梯度。

如果需要计算梯度的Tensor类是一个向量或者是一个矩阵，则需要指定一个与待求导tensor形状匹配的tensor作为backward的输入参数，比如下列程序中的gradient：

import torch

x = torch.randn(2, 2, dtype=torch.double, requires_grad=True)
y = torch.randn(2, 2, dtype=torch.double, requires_grad=True)

def fn():
    return x ** 2 + y * x + y ** 2

gradient = torch.ones(2, 2)

torch.autograd.backward(fn(), gradient, inputs=[x, y])

print(x.grad)
print(y.grad)

grad