PID的局限性

事实上，PID的调参过程就内含对系统进行动力学建模。

以推箱子为例子，PID只会考虑与期望位置的偏差，更为理想的控制应该要估算箱子的重量以及箱子与地面之间的摩擦，从而进行更具有鲁棒性的控制。

一个转动惯量为 $J$ , 包含摩擦 $β$ 、阻尼 $α$ 以及其他未知输入$\gamma $的系统如下

\ddot{θ} = \frac{M_{d r i v e} - α \dot{θ} - β θ - γ}{J}

在控制中，“积分器串联型”系统是很好用的系统。所谓积分器串联型系统如下：

\ddot{θ} = M_{d r i v e}

因此我们自然希望将系统改造成一个积分器串联型的系统。

ADRC

要解决PID的鲁棒性差的问题，我们首先想到的是对系统方程中的转动惯量 $J$ ，摩擦 $β$ 和阻尼 $α$ 进行估计。

假设估计值都使用 $\hat{x}$ 形式表示，我们推导我们的系统方程

\begin{aligned} \ddot{θ} & = \frac{M_{d r i v e} - α \dot{θ} - β θ - γ}{J} \\ = \frac{M_{d r i v e}}{\hat{J}} - \frac{\hat{β}}{\hat{J}} θ + (- \frac{α}{J} \dot{θ} - \frac{γ}{J} + (\frac{1}{J} - \frac{1}{\hat{J}}) M_{d r i v e} + (\frac{\hat{β}}{\hat{J}} - \frac{β}{J}) θ \\ = \frac{M_{d r i v e}}{\hat{J}} - \frac{\hat{β}}{\hat{J}} θ + f \end{aligned}

其中 $f$ 称为“总扰动”

设 $y = θ U = M_{d r i v e}$ , 则我们可以得到标准的模型公式

\ddot{y} = \frac{U}{\hat{J}} - \frac{\hat{β}}{\hat{J}} y + f

如果令输入 $U = \hat{h} (M_{d r i v e 0} + \frac{\hat{β}}{\hat{J}} y - \hat{f})$

代入系统方程，如果 $\hat{f} \to f$ 则可以得到

\ddot{y} \approx M_{d r i v e 0}

对于这样的二阶积分系统，使用简单的PD控制器, 如 $M_{d r i v e 0} = k_{p} (y_{r} - y) - k_{d} \dot{y}$ ，即可实现控制

设状态量

{\begin{array}{r} y = x_{1} \\ \dot{y} = x_{2} \end{array}

则状态模型写为

{\begin{aligned} \dot{x_{1}} & = x_{2} \\ \dot{x_{2}} & = \frac{U}{\hat{J}} - \frac{\hat{β}}{\hat{J}} x_{1} + f \end{aligned}

整个ADRC的思路如下

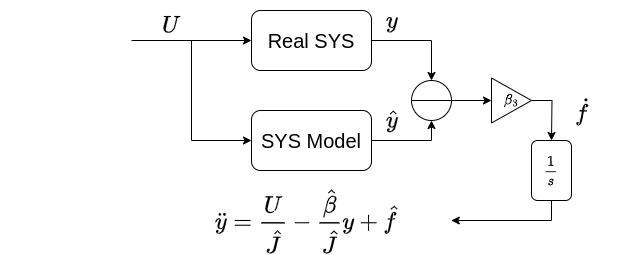
简单来说，就是通过对期望的输出与真实输出的差进行积分实现对SYS Model中总扰动 $\hat{f}$ 的纠错(观测)

这里我们建立一个扩张状态模型，其中总扰动 $f$ 的导数先用 $h$ 代指

{\begin{aligned} \dot{x_{1}} & = x_{2} \\ \dot{x_{2}} & = \frac{U}{\hat{J}} - \frac{\hat{β}}{\hat{J}} x_{1} + f \\ \dot{f} & = h \end{aligned}

基于此我们要构建一个扩张状态观测器。我们是从总扰动 $f$ 的观测开始写, 进一步，写出另外两个状态量的观测方程

\begin{aligned} {\dot{\hat{x}}}_{1} & = {\hat{x}}_{2} + β_{1} (x_{1} - {\hat{x}}_{1}) \\ {\dot{\hat{x}}}_{2} & = \frac{U}{\hat{J}} - \frac{\hat{β}}{\hat{J}} {\hat{x}}_{1} + f_{0} + \hat{f} + β_{2} (x_{1} - {\hat{x}}_{1}) \\ \dot{\hat{f}} & = h - + β_{3} (x_{1} - {\hat{x}}_{1}) \end{aligned}

基于此观测器，我们的控制律设计以及最终闭环动态方程如下

动力学模型： $\ddot{y} = \frac{U}{\hat{J}} - \frac{\hat{β}}{\hat{J}} y - f$

控制律： $u = \frac{u_{0} + \frac{\hat{β}}{\hat{J}} x_{1} + \hat{f}}{1 / \hat{J}} u_{0} = k_{p} (y^{r e f} - y) - k_{d} \dot{y}$

将控制律代入动力学模型，得到闭环系统的动态方程：

\ddot{y} = k_{p} (y^{r e f} - y) - k_{d} \dot{y}

实际值与目标值之间的传递函数为：

\frac{Y}{Y^{r e f}} = \frac{k_{p}}{s^{2} + k_{d} s + k_{p}} = \frac{ω_{n}^{2}}{s^{2} + 2 ξ ω_{n} s + ω_{n}^{2}}

可见，实际值与目标值的比在稳态时为1，动态过程的响应速度及超调量与 $k_{p}$ 和 $k_{d}$ 相关避免超调和振荡，因此令系统的阻尼比 $ξ = 1$ （该过程平滑、无振荡），调节时间约为 $6 ω_{n}$ 。

控制律的调节规律为

k_{p} = ω_{n}^{2} k_{d} = 2 ω_{n} ω_{n} = \frac{6}{τ_{s}}

设 $b_{0} = \frac{1}{\hat{J}} a_{1} = \frac{\hat{β}}{\hat{J}}$ 状态观测器写成矩阵形式如下：

[\begin{matrix} {\dot{\hat{x}}}_{1} \\ {\dot{\hat{x}}}_{2} \\ {\dot{\hat{x}}}_{3} \end{matrix}] = [\begin{matrix} - β_{1} & 1 & 0 \\ - β_{2} + a_{1} & 0 & 1 \\ - β_{3} & 0 & 0 \end{matrix}] [\begin{matrix} {\hat{x}}_{1} \\ {\hat{x}}_{2} \\ {\hat{x}}_{3} \end{matrix}] + [\begin{matrix} β_{1} & 0 & 0 \\ β_{2} & b_{0} & 1 \\ β_{3} & 0 & 0 \end{matrix}] [\begin{matrix} x_{1} \\ u \\ f_{0} \end{matrix}]

至此，我们就只需要选择合适的 $β_{1} β_{2} β_{3}$ 即可

ESO的状态转移矩阵的特征方程如下:

| \begin{matrix} - β_{1} - λ & 1 & 0 \\ - β_{2} + a_{1} & - λ & 1 \\ - β_{3} & 0 & - λ \end{matrix} | = 0

化简得

λ^{3} + β_{1} λ^{2} - (a_{1} - β_{1}) λ + β_{3} = 0

我们通常希望ESO无超调且快速响应，因此不妨令三个极点相同(设为 $ω_{0}$ )。因此状态转移矩阵的特征值相同。

令 $(λ + ω_{o})^{3} = 0$ , 可以解得

{\begin{aligned} β_{1} & = 3 ω_{o} \\ β_{2} & = a_{1} + 3 ω_{o}^{2} \\ β_{3} & = ω_{o}^{3} \end{aligned}

所以，我们只需要确认观测器的极点 $ω_{o}$ ，就能确定观测器的各个系数。在控制系统中，观测器收敛速度必须比控制器快，所以 $ω_{o}$ 通常选择 $3 \sim 5$ 倍的 $ω_{n}$